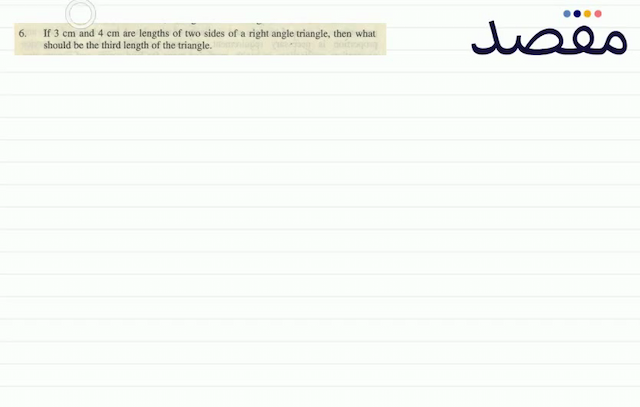
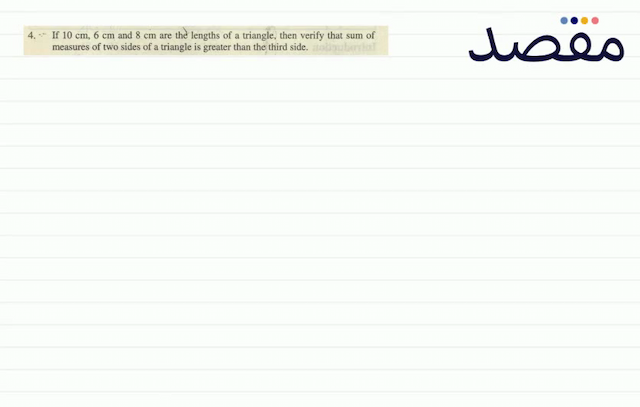
Classes
Class 9 Math Sides and Angles of Triangle
Change the way you learn with Maqsad's classes. Local examples, engaging animations, and instant video solutions keep you on your toes and make learning fun like never before!
Class 9Class 10First YearSecond Year