Classes
Second Year Math Introduction to Analytic Geometry
Change the way you learn with Maqsad's classes. Local examples, engaging animations, and instant video solutions keep you on your toes and make learning fun like never before!
Class 9Class 10First YearSecond Year
Find the lines represented by each of the following and also find measure of the angle between them (Problems 1-6):8. Find a joint equation of the lines through the origin and perpendicular to the lines:\[a x^{2}+2 h x y+b y^{2}=0\]
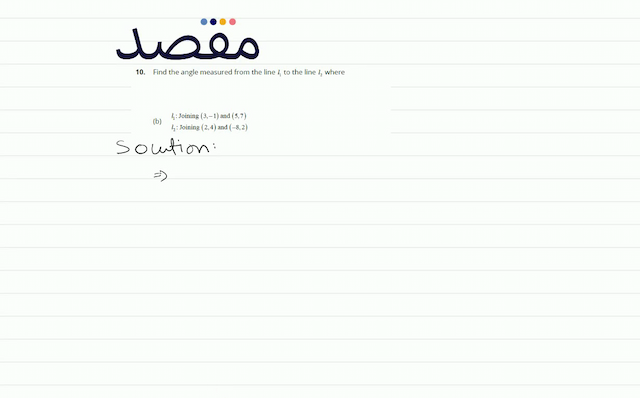
10. Find the angle measured from the line l_{1} to the line l_{2} where(a)\[\begin{array}{l}l_{1}: \text { Joining }(27) \text { and }(710) \\l_{2}: \text { Joining }(11) \text { and }(-53)\end{array}\]
10. Find the angle measured from the line l_{1} to the line l_{2} where(a)\[\begin{array}{l}l_{1}: \text { Joining }(27) \text { and }(710) \\l_{2}: \text { Joining }(11) \text { and }(-53)\end{array}\]


![10. Find the angle measured from the line l_{1} to the line l_{2} where(a)\[\begin{array}{l}l_{1}: \text { Joining }(27) \text { and }(710) \\l_{2}: \text { Joining }(11) \text { and }(-53)\end{array}\]](/_next/image?url=https%3A%2F%2Fmaq-website-bucket-release.s3.ap-southeast-1.amazonaws.com%2Fdoubtsolve%2Fthumbnail-DS_Q_XII_Ex4.4_Q10a.png&w=640&q=75)