Waves | Types, Properties, Examples

Waves are an integral part of understanding the physical world, and they play a crucial role in various scientific and practical applications. From the gentle ripples in a pond to the complex electromagnetic waves that enable wireless communication, waves are everywhere. They are classified into two main types: longitudinal waves and transverse waves, each with distinct characteristics and behaviors. For instance, sound waves, which are examples of longitudinal waves, travel through mediums like air and water, while transverse waves, such as light waves, oscillate perpendicular to their direction of propagation.

Understanding the difference between transverse and longitudinal waves is essential for grasping concepts in physics, engineering, and even seismology, where seismic waves are studied to predict earthquakes. These wave types also form the foundation for exploring advanced topics like electromagnetic waves, which are pivotal in technologies ranging from radio transmissions to medical imaging. By delving into the nature of waves, their classifications, and real-world examples, we can better appreciate their significance and the science behind their behavior.

In this blog post, we will explore the fascinating world of waves, focusing on their types, properties, and applications. Whether you're curious about how sound waves travel or want to differentiate between longitudinal and transverse waves, this guide will provide clarity and insight into the dynamic realm of wave phenomena.

Table of Contents

Oscillatory Motion and Key Terminologies
Simple Harmonic Motion (SHM) and Conditions
Energy Conservation in SHM
Damped and Undamped Oscillations
Resonance and Its Applications
Mechanical Waves: Types and Characteristics
Speed of Sound and Laplace's Correction
Wave Phenomena: Superposition, Beats, and Stationary Waves
Doppler Effect and Frequency Changes

Definition

Waves are disturbances or oscillations that transfer energy from one point to another without the transport of matter. They are broadly categorized into two types: transverse waves, where particle motion is perpendicular to the direction of wave propagation (e.g., electromagnetic waves), and longitudinal waves, where particle motion is parallel to the direction of wave propagation (e.g., sound waves). Waves can also be classified based on their medium, such as mechanical waves requiring a medium (e.g., seismic waves) and electromagnetic waves that can travel through a vacuum. Understanding the difference between transverse and longitudinal waves is crucial for studying phenomena like sound waves, seismic activity, and light propagation.

A diagram illustrating a wave

Oscillatory Motion and Key Terminologies

Oscillatory Motion: The Foundation of Waves 🌊

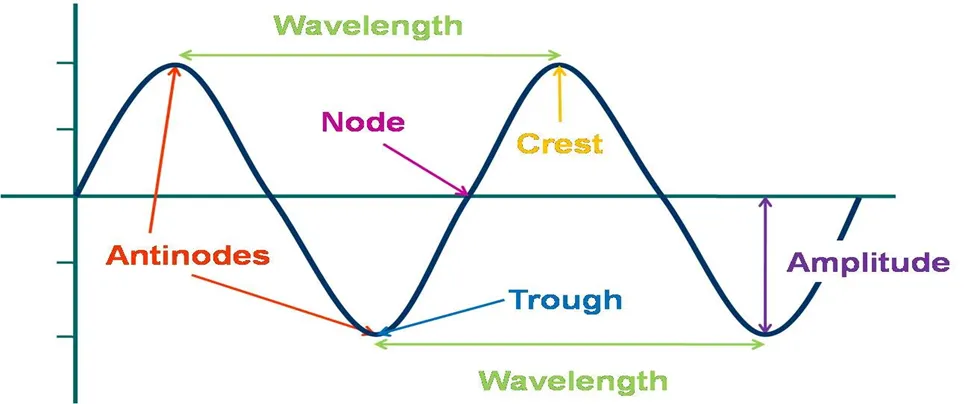
Oscillatory motion is a fascinating concept that forms the backbone of many phenomena in physics. It describes the repetitive back-and-forth movement of an object around a mean position. But what makes this motion so special? Let’s dive into its key aspects and terminologies!

🔑 Key Terminologies in Oscillatory Motion

Understanding oscillatory motion starts with familiarizing yourself with its core concepts. Here are the most important terms:

Time Period (T):
- This is the time taken to complete one full cycle of oscillation.
- For example, the time it takes for a pendulum to swing back and forth once is its time period.
Frequency (f):
- Frequency measures the number of oscillations per unit time and is expressed in Hertz (Hz).
- Fun fact: 1 Hz means one oscillation per second!
Amplitude ( $x_o$ ):
- Amplitude refers to the maximum displacement of the object from its mean position.
- Think of a swing—how far it moves from its resting position is its amplitude.
Angular Frequency ( $\omega$ ):
- Angular frequency connects oscillatory motion to circular motion. It’s calculated using the formula:
  $\omega = 2\pi f$
- This term is especially useful when studying waves like electromagnetic waves.

🛠 Examples of Oscillatory Motion

Oscillatory motion is everywhere! Here are some examples to help you visualize it:
- Swinging of a pendulum: A classic example of periodic motion.
- Vibration of molecules: Molecules oscillate in solids, contributing to their thermal properties.
- Spring-mass system: When a spring is stretched or compressed, it oscillates back and forth.

Connection Between Oscillatory Motion and Waves 🌐

Oscillatory motion is the building block of waves. Waves are essentially oscillations that travel through space and time, carrying energy. Let’s explore some types of waves and their connection to oscillatory motion:

Sound Waves

Sound waves are longitudinal waves, meaning the oscillations occur parallel to the direction of wave propagation. For example:
- When you speak, the air particles vibrate back and forth, creating sound waves that travel to your listener.

Electromagnetic Waves

Electromagnetic waves, like light and radio waves, are transverse waves. Here, the oscillations are perpendicular to the direction of wave travel. These waves are crucial in technologies like:
- Ultrasound imaging
- Seismic wave analysis

Seismic Waves

Seismic waves are generated during earthquakes and include both longitudinal and transverse wave components. They help scientists study the Earth’s interior.

Transverse vs. Longitudinal Waves: What’s the Difference? 🤔

To differentiate between longitudinal and transverse waves, consider the direction of oscillation:
- Transverse Waves: Oscillations are perpendicular to wave propagation. Example: Light waves.
- Longitudinal Waves: Oscillations are parallel to wave propagation. Example: Sound waves.

This distinction is key to understanding how energy moves through different mediums.

Why Oscillatory Motion Matters 🌟

Oscillatory motion isn’t just a physics concept—it’s a gateway to understanding waves. From the examples of longitudinal waves like sound to transverse wave examples like light, oscillatory motion explains how energy travels and interacts with the world around us.

Whether it’s analyzing seismic waves during earthquakes or exploring electromagnetic waves in communication systems, oscillatory motion plays a pivotal role in science and technology. So next time you see a pendulum swing or hear music, remember—you’re witnessing oscillatory motion in action! 🎶

Examples

The swinging of a pendulum is an example of oscillatory motion, where the bob moves back and forth about its mean position, demonstrating periodic cycles.
A spring-mass system exhibits oscillatory motion when the mass is displaced and released, causing it to move repeatedly between its extreme positions.
Sound waves, which are longitudinal waves, originate from oscillatory motion as air molecules vibrate back and forth along the direction of wave propagation.
Seismic waves caused by earthquakes involve oscillatory motion, where the ground moves in repetitive patterns, producing both transverse and longitudinal waves.
Electromagnetic waves, such as light, are formed by oscillatory motion of electric and magnetic fields perpendicular to each other and the direction of wave propagation.

Diagrams depicting simple harmonic motion; left shows circular motion with time segments and right shows the corresponding displacement graph. — Illustration of simple harmonic motion with a circular motion representation on the left and a graph of displacement versus time on the right.

Simple Harmonic Motion (SHM) and Conditions

🌊 What is Simple Harmonic Motion (SHM)?

Simple Harmonic Motion (SHM) is a fascinating type of oscillatory motion that forms the backbone of many wave phenomena, including sound waves and electromagnetic waves. In SHM, the restoring force acting on an object is:

Directly proportional to its displacement from the equilibrium position.
Always directed towards the mean position, ensuring the object oscillates back and forth.

This type of motion is beautifully predictable and is often represented by sinusoidal equations that describe how displacement, velocity, and acceleration change over time.

🛠️ Conditions for SHM

For an object to exhibit SHM, certain conditions must be met:

Inertia
- The object must have inertia to keep moving once displaced. Without inertia, the motion would stop immediately after the initial force is applied.
Restoring Force
- A force proportional to the displacement must act towards the mean position. This force is what 'pulls' the object back, creating oscillations.
Frictionless System
- Ideally, the system should have minimal or no energy loss due to friction. Friction dampens the motion, preventing true SHM.

🔍 Examples of SHM

SHM can be observed in many physical systems. Here are some classic examples:

Simple Pendulum 🕰️
When displaced, the pendulum swings back and forth due to gravity acting as the restoring force.
Spring-Mass System 🌀
A mass attached to a spring oscillates when stretched or compressed, with the spring's elasticity providing the restoring force.

🌐 SHM and Waves

SHM is deeply connected to the behavior of waves. Here's how:

Sound Waves
The vibrations of air particles in sound waves follow SHM, creating compressions and rarefactions.
Electromagnetic Waves
The oscillations of electric and magnetic fields in electromagnetic waves can be modeled using SHM principles.
Seismic Waves 🌍
SHM helps explain the motion of particles during earthquakes, including longitudinal waves and transverse waves.

🧩 Why is SHM Important?

Understanding SHM is essential for analyzing wave phenomena and resonance in physical systems. It helps differentiate between longitudinal waves (where particles move parallel to wave direction) and transverse waves (where particles move perpendicular to wave direction). For example:

Examples of Longitudinal Waves: Sound waves, seismic P-waves.
Transverse Wave Example: Light waves, seismic S-waves.

By studying SHM, scientists can predict wave behavior, design efficient systems, and even explore the mysteries of the universe through electromagnetic waves.

🌟 Fun Fact: Sinusoidal Motion

The equations governing SHM are based on sine and cosine functions. This is why SHM is often referred to as sinusoidal motion. These equations are not just mathematical—they describe the rhythm of nature itself, from the swing of a pendulum to the vibrations of atoms!

Examples

The oscillation of a simple pendulum is an example of SHM, where the restoring force is provided by gravity and acts towards the mean position.
A spring-mass system exhibits SHM when the spring is stretched or compressed, and the restoring force follows Hooke's Law.
Sound waves in air can be analyzed using SHM principles, as the particles oscillate back and forth in a longitudinal wave pattern.
Electromagnetic waves, though not mechanical, exhibit sinusoidal motion similar to SHM in their electric and magnetic field components.
Seismic waves during an earthquake include longitudinal waves (P-waves) and transverse waves (S-waves), which can be studied using SHM concepts.

Diagram showing a mass connected to a vibrating spring with displacement measurements and forces applied. — Illustration of a mass

Energy Conservation in SHM

Energy Conservation in SHM: A Key to Understanding Waves 🌊

In Simple Harmonic Motion (SHM), energy conservation is the cornerstone of its behavior. This principle is not only fascinating but also crucial for understanding how waves—including sound, seismic, and even electromagnetic waves—propagate through different mediums.

🔄 The Energy Dance: Kinetic vs. Potential Energy

In SHM, the total energy of the system remains constant, oscillating seamlessly between Kinetic Energy (KE) and Potential Energy (PE):

Kinetic Energy (KE):
- Where it's at its peak: The mean position.
- Why: The velocity of the oscillating object is highest here.
- Think of it as: The 'speed zone' of the motion.
Potential Energy (PE):
- Where it's at its peak: The extreme positions.
- Why: Displacement from the mean position is greatest, storing energy like a stretched spring.
- Think of it as: The 'stretch zone' of the motion.

🚀 How Energy Drives Waves

This constant interplay between KE and PE ensures that the system keeps oscillating without needing external energy—as long as damping forces are absent. Here's why this is important for waves:

Sound waves:
Energy transfer occurs as particles oscillate back and forth, mimicking SHM principles.
Seismic waves:
These waves travel through Earth's crust, conserving energy as they move.
Electromagnetic waves:
Even light waves exhibit energy conservation, though their mechanism differs slightly from SHM.

🧩 Connecting SHM to Wave Types

Understanding SHM helps us differentiate between longitudinal waves and transverse waves:

Longitudinal Waves:
- Example: Sound waves.
- Energy oscillates parallel to the direction of wave propagation.
Transverse Waves:
- Example: Electromagnetic waves.
- Energy oscillates perpendicular to the direction of wave propagation.

💡 Fun Fact: The difference between transverse and longitudinal waves lies in how energy moves—this is directly tied to the principles of SHM!

🌟 Real-Life Applications of SHM Energy Conservation

Seismic waves: Predicting earthquakes relies on understanding how energy propagates through Earth's layers.
Sound waves: Musical instruments use SHM principles to produce harmonious tones.
Electromagnetic waves: Technologies like Wi-Fi and radio signals depend on energy transfer without loss.

By grasping the energy conservation in SHM, you unlock a deeper understanding of waves and their incredible ability to transfer energy across vast distances—whether it's a ripple in a pond or the light from a distant star. 🌟

A graph illustrating conservation of energy showing total energy with kinetic and potential energy curves over displacement. — Graphical representation of the conservation of energy in a system, displaying kinetic energy (K.E.) and potential energy (P.E.) over displacement.

Damped and Undamped Oscillations

Understanding Damped and Undamped Oscillations 🌊

Oscillations are everywhere—from the gentle sway of a pendulum to the vibrations of sound waves. But did you know they can be categorized based on how energy is lost during motion? Let’s dive into the fascinating world of damped and undamped oscillations.

🔹 Undamped Oscillations

Undamped oscillations occur when there’s no energy loss during motion. This means the amplitude (the maximum displacement from equilibrium) stays constant over time.

Key Characteristics:
- Energy Conservation: All energy remains within the system, enabling continuous oscillation.
- Ideal Conditions: These oscillations are theoretical and occur in environments free of friction or resistance.
- Examples:
- A pendulum swinging in a vacuum 🌌.
- Electromagnetic waves traveling through space without interference.

🔹 Damped Oscillations

Damped oscillations are more common in the real world. Here, the amplitude gradually decreases due to energy loss caused by factors like friction, air resistance, or material properties.

Key Characteristics:
- Energy Dissipation: Energy leaks out of the system, often as heat or sound.
- Real-Life Applications: Damping is critical for controlling vibrations and ensuring stability in various systems.
- Examples:
- A pendulum swinging in air 🌬️.
- Sound waves traveling through a medium, losing intensity over distance.
- Seismic waves dissipating energy as they pass through the Earth 🌍.

Why Is Damping Important?

Damping isn’t just a scientific curiosity—it’s a practical necessity! Here’s why:
- Building Safety: Engineers use damping techniques to reduce vibrations in skyscrapers during earthquakes (seismic waves).
- Acoustics: Damping helps optimize sound wave propagation, ensuring clarity and reducing noise.
- Wave Control: From electromagnetic waves to longitudinal and transverse waves, understanding damping allows us to design systems that balance resonance and stability.

How Do These Oscillations Relate to Waves? 🌊

Oscillations are the backbone of wave motion. Whether it’s longitudinal waves (like sound waves) or transverse waves (like light waves), the principles of damping and undamping influence how waves behave:
- Undamped Waves: Idealized waves, such as electromagnetic waves in space, maintain their energy and amplitude over long distances.
- Damped Waves: Real-world examples include sound waves losing intensity or seismic waves spreading their energy across the Earth.

Fun Fact 💡

Did you know that the difference between transverse and longitudinal waves lies in how particles move? In transverse waves, particles move perpendicular to the wave direction, while in longitudinal waves, they move parallel!

Understanding the difference between damped and undamped oscillations—and how they relate to wave motion—helps us design better systems, whether it’s reducing noise, enhancing resonance, or even protecting buildings during earthquakes. 🌟

Examples

An ideal pendulum swinging in a vacuum demonstrates undamped oscillations, as there is no air resistance to dissipate energy.
A pendulum swinging in air exhibits damped oscillations, where friction with air gradually reduces its amplitude over time.
Seismic waves traveling through the Earth's crust can be damped due to the absorption of energy by the surrounding materials, reducing their intensity.
Sound waves in a concert hall are often damped using acoustic panels to minimize echo and optimize sound quality.
Electromagnetic waves propagating through a vacuum experience no damping, maintaining their amplitude over long distances.

Graph showing amplitude decrease of a damped harmonic oscillator over time with labeled axes. — Graph illustrating the decrease in amplitude of oscillations due to damping forces such as friction and air resistance over time.

Resonance and Its Applications

What is Resonance? 🌊

Resonance is a fascinating phenomenon that occurs when the frequency of an external force aligns perfectly with the natural frequency of a system. This alignment results in a dramatic increase in amplitude, often leading to powerful and sometimes surprising effects. Resonance can be observed in various types of waves, including sound waves, seismic waves, and electromagnetic waves.

Real-Life Applications of Resonance 🔍

Resonance isn't just a theoretical concept—it plays a vital role in many aspects of our daily lives and technological advancements. Here are some notable examples:

1. Bridge Collapse: The Tacoma Narrows Disaster

Resonance can have catastrophic consequences when it comes to structures. In 1940, the Tacoma Narrows Bridge collapsed due to wind-induced resonance, causing the bridge to sway uncontrollably.
Key takeaway: Engineers must carefully account for resonance to prevent structural failures, especially in bridges and skyscrapers.

2. Microwave Ovens: Heating with Electromagnetic Waves

Microwaves use resonance to heat food efficiently. The electromagnetic waves in a microwave oven are tuned to the natural frequency of water molecules, causing them to vibrate and heat up.
Fun fact: This is why foods with high water content heat faster in a microwave!

3. Musical Instruments: Amplifying Sound Waves

Resonance is the secret behind the rich tones of musical instruments. For example:
- In a guitar, the hollow body amplifies sound waves created by vibrating strings.
- In wind instruments, air columns resonate to produce clear, melodious sounds.
Pro tip: Next time you hear a beautiful melody, thank resonance for the amplified sound!

Why Understanding Resonance Matters 🌟

Resonance isn't just about amplifying or mitigating vibrations—it's about understanding the behavior of waves in different systems. Here's why it’s important:

Seismic Waves: Resonance plays a critical role in earthquake engineering. Structures must be designed to withstand the resonance effects of seismic waves to prevent damage.
Sound Wave Amplification: Resonance is used in designing speakers and microphones to enhance sound quality.
Wave Analysis: Differentiating between longitudinal and transverse waves helps scientists predict resonance effects in various environments.

Types of Waves and Resonance 🌀

Resonance can occur in different types of waves, including:

Longitudinal Waves: These waves, like sound waves, involve vibrations parallel to the direction of wave travel. Examples of longitudinal waves include seismic P-waves and sound waves in air.
Transverse Waves: These waves, such as electromagnetic waves, vibrate perpendicular to the direction of wave travel. Transverse wave examples include light waves and water waves.

Understanding the difference between transverse and longitudinal waves is crucial for analyzing resonance in diverse systems.

Fun Fact: Resonance in Everyday Life 🎶

Did you know that resonance is responsible for the clear ringing sound when you tap a wine glass? The glass vibrates at its natural frequency, producing a resonant tone. Try it out—but be careful not to tap too hard, or the glass might shatter due to excessive resonance!

Resonance is a powerful concept that bridges the gap between science and everyday experiences. Whether it's the hum of a guitar string or the efficiency of a microwave oven, resonance reminds us of the incredible behavior of waves in action.

Examples

The Tacoma Narrows Bridge collapse in 1940 is a classic example of resonance, where wind-induced vibrations matched the bridge's natural frequency, causing it to oscillate violently and ultimately fail.
Microwave ovens utilize resonance by emitting electromagnetic waves at a frequency that excites water molecules, efficiently heating food.
In musical instruments like guitars, resonance amplifies sound waves when the strings vibrate at frequencies matching the natural frequency of the instrument's body.
Seismic waves can cause resonance in buildings, leading to amplified vibrations during earthquakes, which engineers must account for in structural designs.
Sound waves in organ pipes create resonance, producing distinct musical notes based on the pipe's length and shape.

Diagram showing a string vibrating in one loop with incident and reflected waves, indicating their wavelengths and points of resonance. — Illustration of a string vibrating in one loop with incident and reflected waves labeled, showcasing the concept of wave frequency and wavelength.

Mechanical Waves: Types and Characteristics

Mechanical Waves: Types and Characteristics 🌊

Mechanical waves are fascinating phenomena that require a medium—like air, water, or solid materials—for their propagation. Unlike electromagnetic waves, they cannot travel through a vacuum. Let’s dive deeper into their types and key characteristics!

Types of Mechanical Waves

Mechanical waves are broadly classified into two types based on how particles of the medium move relative to the wave's direction:

Transverse Waves 🌀
- In transverse waves, the particles of the medium move perpendicular to the direction of wave propagation.
- Imagine ripples on a pond or the oscillation of a string—these are classic examples of transverse waves.
- Examples:
- Water waves 🌊
- Electromagnetic waves (though technically not mechanical, they often serve as a comparison).
Longitudinal Waves 🎵
- Here, the particles of the medium move parallel to the direction of wave propagation.
- Think of compressions and rarefactions in a slinky or sound traveling through air.
- Examples:
- Sound waves 🔊
- Seismic P-waves 🌍

Key Characteristics of Mechanical Waves

Every mechanical wave has unique properties that define its behavior. These include:

Amplitude:
The maximum displacement of particles from their rest position. A higher amplitude means a louder sound or bigger wave ripples!
Frequency:
The number of wave cycles that pass a point in one second, measured in Hertz (Hz). Higher frequency waves often have higher pitches or faster oscillations.
Wavelength:
The distance between two consecutive crests (in transverse waves) or compressions (in longitudinal waves).
Speed:
The rate at which the wave travels through the medium. This depends on the type of medium—waves move faster in solids than in gases!

Why Understanding Mechanical Waves Matters

Mechanical waves play a critical role in various applications:
- Sound wave analysis: From music production to medical ultrasounds, understanding sound waves is essential.
- Seismic wave detection: Longitudinal and transverse waves help scientists study earthquakes and the Earth's structure.
- Wave differentiation: Knowing the difference between transverse and longitudinal waves aids in fields like physics, engineering, and even oceanography.

Fun Fact 💡

Did you know that while sound waves are longitudinal, water waves are a mix of both transverse and longitudinal motions? This combination creates the mesmerizing patterns we see on the surface!

By exploring the examples of longitudinal waves and transverse wave examples, you can better appreciate how these waves shape our world—from the hum of music to the rumble of earthquakes. 🌍✨

Examples

When you drop a pebble into a pond, the ripples created are transverse waves, as the water particles move up and down perpendicular to the direction of wave propagation.
Sound waves traveling through air are longitudinal waves, where air particles vibrate parallel to the direction of wave movement.
Electromagnetic waves, like light, are transverse waves that do not require a medium for propagation, unlike mechanical waves.
Seismic P-waves are longitudinal waves that travel through the Earth's interior, compressing and expanding the material they pass through.
A slinky toy demonstrates both types of waves: stretch and compress it to show longitudinal waves, or shake it side to side to create transverse waves.
Ocean waves are transverse waves where water particles move in circular motions perpendicular to the wave's direction.
The difference between transverse and longitudinal waves can be observed by comparing water waves (transverse) and sound waves (longitudinal).
In a stadium wave, people stand up and sit down in sequence, creating a transverse wave as the motion is perpendicular to the direction of propagation.

Diagram illustrating sound wave propagation with areas of compressions and rarefactions. — Illustration depicting sound wave propagation, showing areas of compressions and rarefactions.

Speed of Sound and Laplace's Correction

Understanding the Speed of Sound: Newton's Formula vs. Laplace's Correction 🌊

The speed of sound is a fascinating concept that depends on the properties of the medium through which it travels. Specifically, it is influenced by the medium's elasticity (how easily it can return to its original shape) and density (how tightly packed its particles are). Let's dive deeper into this topic and explore the groundbreaking contributions of Newton and Laplace.

🧠 Newton's Formula for Sound Speed

Newton initially proposed that sound waves travel under isothermal conditions—where the temperature remains constant during compression and rarefaction. His formula is:

$v = \sqrt{P/\rho}$

Here:
- $v$ = speed of sound
- $P$ = pressure of the medium
- $\rho$ = density of the medium

While this formula was a significant step forward, it produced results that didn't match experimental observations. Why? Because sound waves actually propagate under adiabatic conditions, where heat exchange doesn't occur during the process.

🔧 Laplace's Correction: The Game-Changer

Laplace corrected Newton's formula by accounting for the adiabatic nature of sound wave propagation. He introduced the adiabatic index ( $\gamma$ ), which represents the ratio of specific heats of the medium. The corrected formula is:

$v = \sqrt{\gamma P/\rho}$

This adjustment made calculations far more accurate and aligned with experimental data. Here's what each term means:
- $\gamma$ = adiabatic index (specific to the medium, e.g., 1.4 for air)
- $P$ = pressure
- $\rho$ = density

🌡️ Factors Influencing the Speed of Sound

The speed of sound isn't fixed—it changes depending on several factors. Here are the most important ones:

Temperature: Higher temperatures increase the speed of sound because particles move faster, enhancing wave propagation.
Humidity: Moist air (with higher water vapor content) reduces density, allowing sound to travel faster.
Wind Direction: Wind can either aid or hinder sound waves, depending on whether it moves in the same direction as the wave.

🌍 Applications of Sound Speed in Real Life

Understanding the speed of sound has practical uses across various fields:
- Acoustic Engineering: Designing concert halls and speaker systems to optimize sound quality.
- Medical Imaging: Using sound waves (like ultrasound) to create detailed images of internal organs.
- Seismic Wave Analysis: Studying earthquakes and the Earth's interior by analyzing the speed of seismic waves.

🌀 Sound Waves vs. Other Waves

Sound waves are a type of longitudinal wave, where particles vibrate parallel to the wave's direction of travel. This contrasts with transverse waves, where particles move perpendicular to the wave direction. For example:
- Examples of longitudinal waves: Sound waves, seismic P-waves.
- Transverse wave example: Light waves, water waves.

Understanding the difference between transverse and longitudinal waves is crucial for fields like physics and engineering, as each type behaves uniquely.

By exploring the speed of sound and Laplace's correction, we gain deeper insights into how waves behave in different media. Whether you're studying sound waves, seismic waves, or even electromagnetic waves, this knowledge is essential for unraveling the mysteries of wave propagation.

Diagram of a wave pattern with labeled nodes and antinodes along the wavelength. — Illustration of a wave pattern showing nodes and antinodes along a wavelength.

Comparison of Newton's Formula and Laplace's Correction for Sound Speed

This table compares Newton's formula and Laplace's correction for calculating the speed of sound in waves. It highlights the differences in assumptions, accuracy, and applications, aiding in understanding sound wave propagation and seismic wave analysis.
Aspect	Newton's Formula	Laplace's Correction
Formula	$v = \sqrt{P/\rho}$	$v = \sqrt{\gamma P/\rho}$
Assumption	Isothermal conditions	Adiabatic conditions
Accuracy	Inaccurate results	Accurate results
Key Parameter	Pressure (P) and Density (ρ)	Pressure (P), Density (ρ), and Adiabatic Index (γ)
Applications	Basic sound speed estimation	Precise calculations for acoustic engineering and medical imaging

Wave Phenomena: Superposition, Beats, and Stationary Waves

🌊 Understanding Wave Phenomena: Superposition, Beats, and Stationary Waves

Wave phenomena are fascinating interactions that occur when multiple waves meet. These principles are not only essential for understanding the behavior of waves but also have practical applications in fields like music, acoustics, and even geology. Let’s dive into the details!

📌 1. Superposition Principle

The superposition principle is the foundation of wave interactions. It states that:

The resultant displacement at any point is the sum of the displacements of individual waves passing through that point.

Here’s how it works:
- If two waves meet and their crests align, they create a larger wave (constructive interference).
- If a crest meets a trough, the waves cancel each other out (destructive interference).

This principle applies to sound waves, electromagnetic waves, and even seismic waves, making it crucial for understanding phenomena like noise cancellation and light diffraction.

🎶 2. Beats: The Rhythmic Pulse of Waves

Ever wondered how musicians tune their instruments? That’s where beats come in!

What are beats?
Beats occur when two waves with slightly different frequencies overlap. The result is a rhythmic variation in amplitude, creating a 'pulsing' sound.
Why are beats important?
- Used in tuning musical instruments to achieve perfect harmony.
- Helps engineers design acoustic systems with precise frequency control.

🎵 Fun Fact: The closer the frequencies, the slower the beats. This is why tuning requires careful adjustments!

🌟 3. Stationary Waves: Waves That Stand Still

Stationary waves, also known as standing waves, are formed when two identical waves travel in opposite directions and interfere.

Key features of stationary waves:
- Nodes: Points where the wave amplitude is zero (complete destructive interference).
- Antinodes: Points of maximum amplitude (constructive interference).
Applications:
- Designing musical instruments like guitars and violins, where strings vibrate to produce stationary waves.
- Optimizing acoustic systems in concert halls.
- Analyzing seismic waves to study Earth's structure.

🌎 Applications Across Wave Types

Wave phenomena aren’t limited to sound waves—they extend to electromagnetic waves, longitudinal waves, and transverse waves. Here’s how they’re applied:

Electromagnetic waves: Superposition explains interference patterns in light, used in technologies like lasers and fiber optics.
Seismic waves: Stationary wave analysis helps scientists predict earthquakes and study Earth's layers.
Sound waves: Beats and stationary waves are essential for designing musical instruments and soundproofing systems.

🔍 Quick Comparison: Longitudinal vs. Transverse Waves

Understanding the difference between wave types is key:

ApplicationsUltrasound imaging, seismic analysisLight transmission, ocean wave studies
Feature	Longitudinal Wave	Transverse Wave
Direction of particle motion	Parallel to wave direction	Perpendicular to wave direction
Examples	Sound waves, seismic P-waves	Water waves, electromagnetic waves

Wave phenomena like superposition, beats, and stationary waves are not just theoretical concepts—they’re the backbone of technologies we use every day. Whether it’s tuning a guitar, designing a concert hall, or studying the Earth’s crust, understanding these principles unlocks a world of possibilities! 🌟

Examples

When two sound waves of slightly different frequencies overlap, they produce beats, which are used by musicians to tune instruments accurately.
Seismic waves during an earthquake demonstrate both longitudinal and transverse wave properties, helping geologists analyze Earth's structure.
Electromagnetic waves, like light, exhibit superposition, enabling technologies like interference filters in cameras.
In a stretched string, stationary waves form when identical waves travel in opposite directions, creating nodes and antinodes visible in musical instruments like guitars.
The superposition principle explains how noise-canceling headphones work by creating sound waves that counteract unwanted noise.

Diagram showing a string vibrating in three loops with labeled nodes (N1, N2, N3) and antinodes (A) representing wave motion. — Illustration of a string vibrating in three loops, demonstrating wave patterns and nodes.

Doppler Effect and Frequency Changes

What is the Doppler Effect? 🌊

The Doppler Effect explains how the frequency or wavelength of waves changes when there is relative motion between the source of the waves and the observer. This phenomenon applies to various types of waves, including sound waves, electromagnetic waves, and even seismic waves.

Key Concepts of the Doppler Effect:

Red Shift 🚀: When the source moves away from the observer, the wavelength increases, causing a shift toward the red end of the spectrum. This is commonly observed in electromagnetic waves emitted by stars and galaxies.
Blue Shift 🌌: When the source moves closer to the observer, the wavelength decreases, resulting in a shift toward the blue end of the spectrum.

Real-World Applications of the Doppler Effect 🛠️

The Doppler Effect isn't just a theoretical concept—it has practical uses across multiple fields. Here are some fascinating examples:

1. Astronomy 🌟

Scientists use the Doppler Effect to study the motion of celestial objects.
Red shifts indicate that stars or galaxies are moving away, helping astronomers understand the universe's expansion.
Blue shifts reveal objects moving closer, aiding in the study of gravitational interactions.

2. Medical Imaging 🏥

Doppler ultrasound technology uses sound waves to measure the speed and direction of blood flow in the body.
This technique is crucial for diagnosing conditions like blocked arteries or heart valve issues.

3. Radar Systems 🚗

Police radars and speed detectors rely on the Doppler Effect to measure the velocity of moving vehicles.
Similarly, weather radars use this principle to track storm movements and wind speeds.

How Does the Doppler Effect Relate to Different Types of Waves? 🌊

The Doppler Effect applies to both longitudinal waves (like sound waves) and transverse waves (like electromagnetic waves). Here's how:

Longitudinal Waves: These waves, such as sound waves, compress and expand as they travel. The Doppler Effect changes the pitch of the sound—think of the high-pitched whine of a car passing by.
Transverse Waves: These waves, like light or radio waves, oscillate perpendicular to their direction of travel. The Doppler Effect alters their wavelength, leading to red or blue shifts.

Fun Fact: Seismic Waves and the Doppler Effect 🌍

Even seismic waves, which travel through the Earth's crust during earthquakes, can exhibit Doppler shifts. Scientists use this principle to analyze the movement and intensity of tectonic activity.

Why Understanding the Doppler Effect Matters 🔍

The Doppler Effect is more than just a scientific curiosity—it’s a tool for unlocking the mysteries of the universe, improving medical diagnostics, and enhancing everyday technologies like radar systems. By understanding how waves behave under motion, we gain insights into phenomena ranging from the smallest blood vessels to the largest galaxies.

Related Topics to Explore:

Difference between transverse and longitudinal waves
Examples of longitudinal waves in nature
Transverse wave example in electromagnetic radiation

Dive deeper into the fascinating world of waves and their applications to uncover even more connections between science and everyday life!

Examples

Astronomers use the Doppler Effect to detect red shifts in light waves from distant galaxies, indicating they are moving away from Earth.
In medical imaging, Doppler ultrasound utilizes sound waves to measure blood flow velocity in arteries and veins.
Police radar systems employ the Doppler Effect to calculate the speed of vehicles by analyzing changes in electromagnetic wave frequency.
Seismologists analyze seismic waves using the Doppler Effect to determine the movement and velocity of tectonic plates during earthquakes.
A train horn sounds higher in pitch (blue shift) as it approaches and lower in pitch (red shift) as it moves away, illustrating the Doppler Effect with sound waves.

Formula for calculating the Doppler effect with notes on observer and source movement. — A comprehensive formula for calculating the Doppler effect, including notes on how to determine the sign based on the movement of the source and observer.

Conclusion

In conclusion, understanding waves and their diverse forms—such as electromagnetic waves, longitudinal waves, and transverse waves—is essential for grasping the physical phenomena that govern our world. This blog has explored the fundamental differences between transverse and longitudinal waves, their unique characteristics, and practical examples like seismic waves and sound waves. By mastering these concepts, you not only gain insights into the mechanics of wave propagation but also appreciate their applications in fields ranging from medical imaging to earthquake studies. Whether you're differentiating between longitudinal and transverse waves or examining real-world examples, waves remain a cornerstone of both theoretical and applied physics.

FAQs

Q: What are waves in physics?

A: Waves are disturbances that transfer energy from one place to another without transferring matter. They can be classified into mechanical waves, such as sound waves, and electromagnetic waves, such as light waves.

Q: What is the difference between transverse and longitudinal waves?

A: Transverse waves have oscillations perpendicular to the direction of wave propagation, like electromagnetic waves. Longitudinal waves have oscillations parallel to the direction of wave propagation, like sound waves.

Q: Can you provide examples of longitudinal waves?

A: Examples of longitudinal waves include sound waves, seismic P-waves, and compression waves in springs.

Q: What are transverse waves and their examples?

A: Transverse waves are waves where the oscillations are perpendicular to the direction of propagation. Examples include electromagnetic waves, water waves, and light waves.

Q: How do electromagnetic waves differ from mechanical waves?

A: Electromagnetic waves do not require a medium to propagate and can travel through a vacuum, while mechanical waves, such as sound waves, require a medium like air, water, or solid materials.

Q: What are seismic waves and their types?

A: Seismic waves are waves generated by earthquakes or other geological activities. They are classified into primary waves (P-waves), which are longitudinal, and secondary waves (S-waves), which are transverse.

Q: What factors affect the speed of sound waves?

A: The speed of sound waves is influenced by the medium's elasticity, density, temperature, and humidity. For instance, sound travels faster in solids than in gases due to higher elasticity.

Q: Why are electromagnetic waves considered transverse waves?

A: Electromagnetic waves are transverse because their electric and magnetic fields oscillate perpendicular to the direction of wave propagation.

Q: What is the principle of superposition in wave phenomena?

A: The principle of superposition states that when two or more waves overlap, the resulting displacement at any point is the sum of the displacements due to each individual wave.

Q: How do longitudinal and transverse waves differ in terms of particle motion?

A: In longitudinal waves, particles move parallel to the wave's direction of propagation. In transverse waves, particles move perpendicular to the wave's direction of propagation.